УДК 681.7
© И.О. Михайлов
Сибирская государственная геодезическая академия
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
ФОКОМЕТРА
Ход луча света после прохождения
оптического силового компонента можно описать линейной функцией
вида (рис. 1)
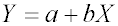 , ,
|
(1) |
Если задняя главная точка линзы
помещается в начало координат, то луч с началом в точке А
подчиняется формуле (1), а угол его наклона зависит от фокусного
расстояния f ' линзы и пересекает ось абсцисс в точке
В с координатой
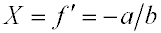 , ,
|
(2) |
где а - коэффициент,
равный высоте падения луча на линзу; b - коэффициент,
зависящий от фокусного расстояния линзы.
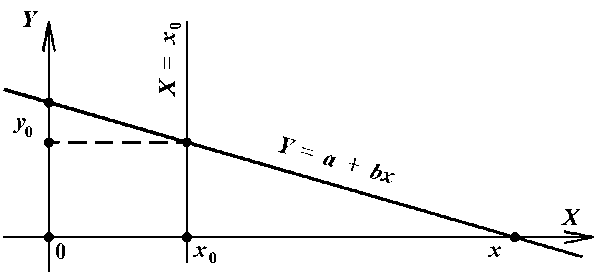
Рис. 1. Графики двух линейных
функций
Для решения уравнения (2) необходимо
определить коэффициент b. Это легко сделать, воспользовавшись
еще одной линейной функцией
 , ,
|
(3) |
Совместное решение уравнений (1)
и (3) дает
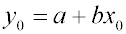 . . |
|
После подстановки отсюда значения
b в выражение (2) получается расчетная формула
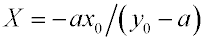 . . |
(4) |
в которой значение Х
определяется в широком диапазоне 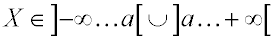 при
при 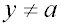 . .
Таким образом, получена функциональная
зависимость Х = f(y0)
или f = f(y0)
при фиксированных значениях а и x0.
Измерив у0, можно определить Х
или f . На рис. 2 представлено решение уравнения при
заданных конструктивных параметрах а = 10 мм, x0
= 10 мм, у0 изменяется в диапазоне
от 0 до 20 мм.
Рис. 2. График уравнения
(4)
График иллюстрирует очевидное
явление: незначительное изменение значения у0
(при 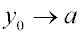 )
приводит к резкому изменению величины X. Кроме того,
в связи с тем, что при )
приводит к резкому изменению величины X. Кроме того,
в связи с тем, что при 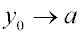 в точке у0 = а происходит
разрыв функции, которая меняет свой знак, для некоторой области
измерений характерны особенно большие погрешности.
в точке у0 = а происходит
разрыв функции, которая меняет свой знак, для некоторой области
измерений характерны особенно большие погрешности.
Из выражения (4) находим
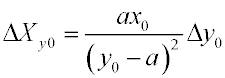 . . |
(5) |
где 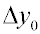 - погрешность, с которой определяется величина у0.
Тогда относительная погрешность определения Х есть
- погрешность, с которой определяется величина у0.
Тогда относительная погрешность определения Х есть
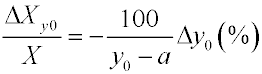 . . |
|
Ее изменение при а =
10 мм, у0 = 0,0015 мм и у0
= 0...20 мм показано на рис. 3. По графику относительной погрешности
определяется диапазон значений у0,
в котором получается необходимая точность измерений при заданных
конструктивных параметрах устройства.
Рис. 3. График относительной
погрешности dX/X
Из формулы (4) видно, что при
изменении величины х0 изменяется
диапазон значений X. Поэтому, построив график функции
(4) при исходных (конструктивных) данных а = 10 мм, у0min
= 0 мм (9 мм), у0max = 11 мм (20
мм) для диапазона х0 от 0 до 2000
мм (рис. 4) и подбирая значение х0,
можно определять значения Х в необходимом диапазоне при
сохранении относительной погрешности не более заданной.
Рис. 4. График функции
(4) заданных значениями a, y0,
x0
Таким образом, можно спроектировать
устройство для измерения фокусного расстояния линзы по схеме рис.
1, если в плоскости с координатой х0
проводятся измерения координаты y0
прохождения светового пучка. При этом учитывается область, в которой
погрешность измерения удовлетворяет требованиям точности (рис.
3), а расположение измерительной плоскости (координата х0)
относительно главной точки линзы определяется по графику рис.
4 в зависимости от ее предполагаемого фокусного расстояния.
Существенным недостатком подобной
схемы является необходимость размещения задней главной точки линзы
точно в начале координат, для чего на практике требуются дополнительные
технические решения (например, вспомогательная зрительная труба,
шкала, поворотный столик), значительно усложняющие конструкцию
и резко снижающие производительность измерений.
Рассмотрим возможность исключения
необходимости совмещения задней главной точки линзы с началом
координат. На рис. 5 в сравнении с рис. 1 введена третья линейная
функция
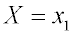 . . |
(6) |
Решением систем уравнений (1),
(3) и (1), (6) определим координаты y0
и y1
 . . |
|
Величина а выражается через уравнения
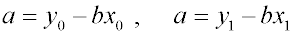 . . |
|
Отсюда
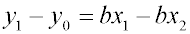 и
и 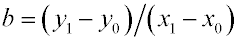 . . |
|
После подстановки в (2) получается
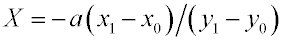 . . |
|
где x1-x0
= l - расстояние между измерительными плоскостями, заданными
функциями Х = х1 и Х
= x0; у1-у0
= у - разность координат у1
и у0 с учетом знака, определенных
в двух измерительных плоскостях. Отсюда
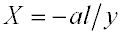 . . |
(7) |
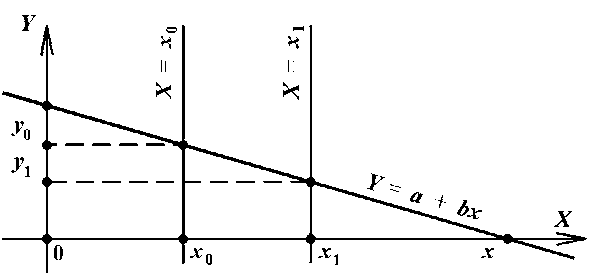
Рис. 5. Графики трех линейных
функций
Погрешность определения величины
Х при погрешности измерения у определяется дифференцированием
выражения (7) по переменной у, а относительная погрешность
определяется из выражения
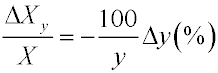 . . |
|
Влияние погрешности аттестации
размера а на погрешность измерения величины Х
определяется дифференцированием формулы (7) по переменной а.
При этом уравнение относительной погрешности
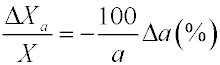 . . |
|
где 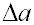 - погрешность аттестации размера а.
- погрешность аттестации размера а.
Для определения диапазона измеряемых
фокусных расстояний с погрешностью не более заданной по формуле
(7) может быть построен соответствующий график (рис.4).
Таким образом, устройство для
измерения фокусного расстояния линз, построенное по схеме рис.
5 с двумя измерительными плоскостями, свободно от необходимости
совмещения задней главной точки линзы с началом системы координат.
В данном устройстве необходимо с высокой степенью точности определять
расстояние l между измерительными плоскостями, которое
постоянно и является конструктивным параметром данного устройства.
Среднеквадратическое отклонение
(СКО) устройства определяется по формуле
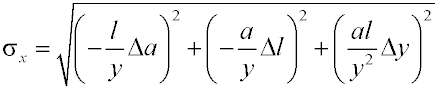 . . |
(8) |
где 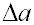 - погрешность определения величины а;
- погрешность определения величины а; 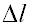 - погрешность определения величины l,
- погрешность определения величины l, 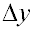 - погрешность определения величины у.
- погрешность определения величины у.
При заданных конструктивных параметрах
устройства, например, a = 10 мм, l = 10мм, ymin
= 2 мм (-2 мм), ymax = 10 мм (-10
мм) и погрешностях измерения заданных величин 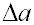 = 0,001 мм,
= 0,001 мм, 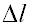 =
0,001 мм, =
0,001 мм, 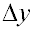 =
0,002 мм по формуле (8) СКО составляет: =
0,002 мм по формуле (8) СКО составляет:
Хmax
= 50 мм, 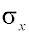 =
0,1002 мм или =
0,1002 мм или 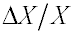 =
0,2%; =
0,2%;
Хmin = 10 мм, 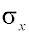 =
0,0042 мм или =
0,0042 мм или 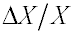 =
0,04%. =
0,04%.
Аналогично при а = 10 мм и l = 200:
Хmax = 1000 мм, 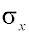 =
2,002 мм или =
2,002 мм или 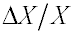 =
0,2%; =
0,2%;
Хmin = 200 мм, 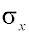 =
0,0824 мм или =
0,0824 мм или 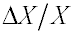 =
0,04%. =
0,04%.
Точные измерения фокусного расстояния
линз осложняются наличием продольной сферической аберрации. Плоскость
Гаусса соответствует положению изображения точки расположенной
в бесконечности и построенной параксиальным пучком лучей. Поэтому
в устройстве для измерения фокусного расстояния по схемам рис.
1 и рис. 5 высота а падения луча на линзу берется с учетом сферической
аберрации.
Влияние сферической аберрации
удобнее проанализировать по отношению продольной сферической аберрации
линзы к ее фокусному расстоянию S' /F' . Эта
величина является относительной погрешностью определения фокусного
расстояния по схеме рис. 5.
Принципиальная оптическая схема
устройства представлена на рис. 6. Из широкого параллельного пучка
лучей непрозрачным экраном 1 с двумя узкими параллельными щелями
вырезаются пучки света, расположенные на расстоянии 2а
друг от друга. Узкие пучки падают на контролируемую деталь 2,
после прохождения которой отклоняются на некоторый угол и пересекают
измерительные плоскости I и II, где определяются координаты следов
световых пучков. Расстояние l между плоскостями I и II
- конструктивный параметр устройства, заранее установленный с
необходимой точностью. Наличие двух измерительных каналов (двух
пучков лучей) позволяют компенсировать погрешность децентрировки
щелей экрана относительно оптической оси контролируемого компонента,
так как учитывается среднее значение у определенных в
обоих каналах.
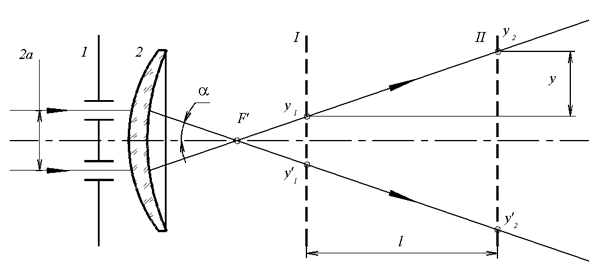
Рис. 6. Принципиальная
схема фокометра
Из изложенного выше вытекает методика
определения конструктивных параметров устройств (рис. 6), предназначенных
для определения фокусных расстояний силовых компонентов оптических
систем, при этом начальным условием является относительная погрешность
измерения и диапазон фокусных расстояний контролируемых компонентов.
Параметры определяются в последовательности:
- при заданной относительной погрешности
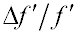 измерения
фокусного расстояния определяется минимальное значение ymin,
при котором обеспечивается необходимая точность измерений измерения
фокусного расстояния определяется минимальное значение ymin,
при котором обеспечивается необходимая точность измерений
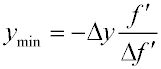 . . |
|
- определяется высота падения
луча а с учетом влияния сферической аберрации;
- определяется расстояние l
между измерительными плоскостями в зависимости от предполагаемой
величины фокусного расстояния контролируемой линзы
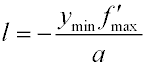 . . |
|
Как показывают результаты анализа,
предложенная методика измерения с использованием двух измерительных
плоскостей дает возможность существенно упростить конструкцию
установки и сократить время ее проектирования, так как:
- нет необходимости базироваться
на заднюю главную точку контролируемого компонента;
- нет необходимости совмещать
какое-либо отсчетное устройство с точ-кой заднего фокуса контролируемого
компонента;
- измерения ведутся вблизи самого
контролируемого компонента, что резко снижает габариты установки;
- нет дополнительного вспомогательного
объектива (в сравнении с методом Фабри-Юдина), который увеличивает
габариты прибора и снижает точность его работы.
© И. О. Михайлов, 2002
|