Критерий согласия хи-квадрат (Пирсона)
Обработка результатов прямых равноточных измерений
Обработка результатов косвенных измерений
Программа статистической обработки измерений
Литература
Цель работы: научиться обрабатывать экспериментальные данные равноточных измерений.
Приборы и принадлежности:
1. Персональный компьютер;
2. Программа статистической обработки экспериментальных данных. Скачать программу.
Измерение – совокупность операций, выполняемых с помощью технического средства, хранящего единицу величины, позволяющего сопоставить измеряемую величину с ее единицей и получить значение величины. Это значение называют результатом измерений.
Результат измерений должен сопровождаться указанием погрешности, с которой он получен.
Погрешность измерений – отклонение результатов измерений от истинного (действительного) значения измеряемой величины.
Истинное значение физической величины неизвестно и применяется в теоретических исследованиях; действительное значение величины определяется экспериментально из предположения, что результат эксперимента (измерения) наиболее близок к истинному значению величины.
Цель любого измерения – это получение результата измерений с оценкой истинного значения измеряемой величины. Для этого проводится обработка результатов измерений, в большинстве случаев с помощью вероятностно-статистических методов теории вероятностей и математической статистики.
Считается, что однократные измерения допустимы только в порядке исключения, так как они по существу не позволяют судить о достоверности измерительной информации. Если можно принять, что в погрешности результата измерений роль систематической [1] погрешности пренебрежимо мала по сравнению со случайной [2] погрешностью, то при определении необходимого количества измерений следует исходить из возможности проведения статистической обработки результатов измерений. Известно, что при 7 … 8 измерениях оценки их результатов приобретают некоторую устойчивость. Если необходимо получение достоверных результатов измерений, то их число должно быть 25 … 30. Если объект измерений до этого не исследовался и, кроме предварительных, обычно расчетных значений величин, о нем мало что известно. В этом случае число измерений должно быть увеличено до 50 … 100, а при необходимости нахождения законов распределения оцениваемых величин число измерений целесообразно увеличить на порядок.
Главная цель увеличения числа измерений (если систематическая составляющая погрешности исключена) состоит в уменьшении случайности результата измерений и, следовательно, в наилучшем приближении результата к истинному значению величины. Но увеличивать число измерений с целью найти истинное значение величины бессмысленно.
По результатам измерений чаще всего рассчитывают среднее арифметическое значение и статистическое среднее квадратическое отклонение (СКО) величины. Первое является оценкой математического ожидания величины, а статистическое СКО – оценкой теоретического СКО.
Пусть изучается некоторая случайная величина x. Произведено n независимых измерений с результатами x1, x2… xi … xn. Для оценки истинного значения измеряемой величины используется среднее арифметическое значение, которое обычно обозначается 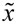 или
или 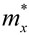 (оценка математического ожидания mx, соответствующего для физической величины ее истинному значению):
(оценка математического ожидания mx, соответствующего для физической величины ее истинному значению):
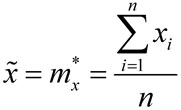 . . |
(1) |
Оценкой дисперсии Dx дискретной величины X является статистическая дисперсия, как статистический второй центральный момент [3]
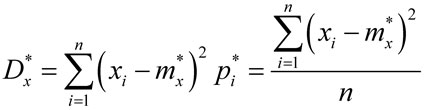 ,
,
где 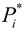 – статистическая вероятность значения xi.
– статистическая вероятность значения xi.
Одним из условий получения надежных оценок является требование к их несмещенности, которое заключается в том, чтобы при замене оценкой 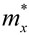 истинного значения Xист не допускалась систематическая погрешность (в сторону увеличения или уменьшения относительно Xист).
истинного значения Xист не допускалась систематическая погрешность (в сторону увеличения или уменьшения относительно Xист).
Несмещенной оценкой дисперсии Dx является величина
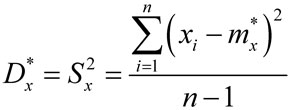 . . |
(2) |
Статистическое СКО
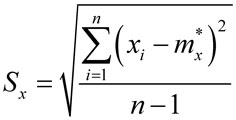 . . |
(3) |
При обработке результатов измерений приходится встречаться с различными законами распределения измеряемых величин, рассматриваемых как случайные величины: нормальный закон распределения, равномерный закон распределения, арксинусный закон распределения, треугольный закон распределения, корреляционный закон распределения.
Нормальный закон распределения величины х представляется плотностью распределения
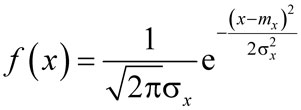 , , |
(4) |
где mx – математическое ожидание величины X;
sх– СКО (теоретическое).
Плотность распределения величины Х является размерной функцией:
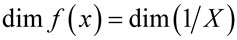 , [4].
, [4].
Кривая плотности распределения величины Х симметрична относительно точки рассеивания, имеющей абсциссу mx (рисунок 1). Параметр sх характеризует форму кривой распределения. С увеличением значения sх кривая распределения «растягивается» вдоль оси абсцисс.
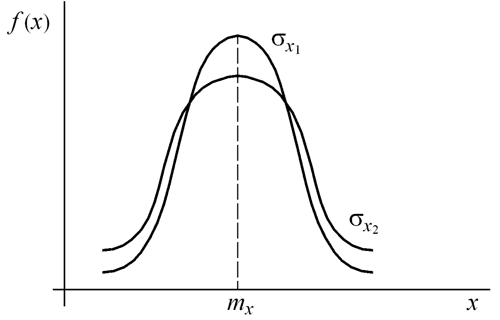
Рисунок 1 - Нормальный закон распределения
Для некоторого интервала значений от a до b вероятность того, что выполняется a < X < b
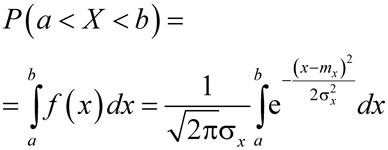 .
.
После замены переменной 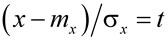 , т.е.
, т.е. 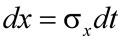 :
:
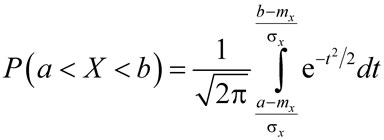 . . |
(5) |
Для вычисления интеграла (5) пользуются таблицами функции Лапласа (приложение А) в виде
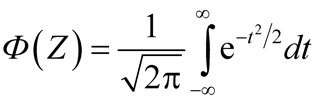 . . |
(6) |
С помощью функции Лапласа вычислен интеграл (5)
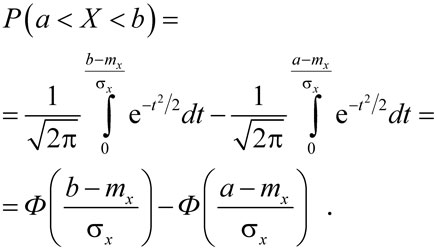 |
(7) |
При выполнении точных измерений целесообразно изучить реальную форму закона распределения результатов измерений и учитывать его свойства при обработке этих результатов.
С целью нахождения закона распределения той или иной величины (параметра) производятся сотни и тысячи измерений. После построения эмпирического закона распределения величины необходимо построить соответствующую ему модель теоретического закона распределения, обычно путем сопоставления эмпирической модели известным законам распределения. Эта задача решается с помощью критериев согласия: критерий согласия хи-квадрат (Пирсона), критерий согласия Колмогорова, метод моментов. В зависимости от применяемых критериев согласия закон распределения представляется в виде плоскости распределения, функции распределения или отношений центральных моментов случайной величины.
Отличаясь простотой применения, критерий Колмогорова уступает критерию хи-квадрат по степени доверия к результатам идентификации законов распределения.
Применение метода моментов требует наличия большого количества измерений. Для надежной оценки первого момента (математического ожидания) требуется выборка n ³ 30, для оценки вторых моментов – n ³ 100, для оценки третьих моментов – n » 1000. Таким образом, применение метода моментов при обычных, небольших выборках (число измерений не превышает 100) практически ограничено.
Во многих случаях число измерений, превышающее 30 … 40, позволяет использовать их результаты для идентификации закона распределения с помощью критерия хи-квадрат.
Пусть произведено n независимых измерений некоторой величины X, рассматриваемой как случайная. Результаты измерений для удобства распределяются в порядке возрастания от наименьшего до наибольшего.
Весь диапазон измеренных значений величины Х разделяется на некоторое число разрядов (интервалов). Число этих разрядов определяется различными способами, например
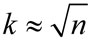 или или 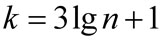 , , |
(8) |
где k – число разрядов;
n – число измерений.
После определения числа разрядов ряда строится статистический ряд – таблица 1, в которой приведены длины разрядов Ii (в порядке их соответствия оси абсцисс измеряемой величины Х), количества значений величины mi, оказавшихся в том или ином разряде, а также статистические частоты P*i.
Таблица 1
Ii |
x1; x2 |
x2; x3 |
- |
xi; xi+1 |
- |
xk; xk+1 |
mi |
m1 |
m2 |
- |
mi |
- |
mk |
|
|
|
- |
|
- |
|
Если теоретический закон нормальный, то с помощью формулы (7) определяется теоретическая вероятность в разряде (xi; xi+1):
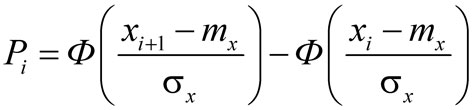 ,
,
где mx и sx – соответственно математическое ожидание и СКО величины Х.
Поскольку они не известны, то при расчетах заменяются статистическими значениями 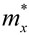 – средним арифметическим значением (1) и статистическим СКО Sx (3).
– средним арифметическим значением (1) и статистическим СКО Sx (3).
В качестве меры расхождения между теоретическими вероятностями и статистическими частотами критерий хи-квадрат предусматривает использование величины
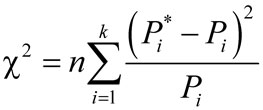 , , |
(9) |
Если в процессе использования критерия согласия хи-квадрат определена величина c2, то по числам c2 и r (r = k – s – число степеней свободы, где s – число независимых условий, которым должны удовлетворять статистические вероятности 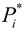 . Число s определяется формой теоретического закона распределения. Для симметричных законов распределения, таких как нормальный, s = 3) с помощью таблицы (приложение Б) находится вероятность р того, что величина, имеющая распределение c2 с r степенями свободы, превзойдет данное значение c2. Вероятность р есть вероятность того что за счет чисто случайных причин мера расхождения теоретического и эмпирического распределений должна быть не меньше, чем полученная по результатам измерения.
. Число s определяется формой теоретического закона распределения. Для симметричных законов распределения, таких как нормальный, s = 3) с помощью таблицы (приложение Б) находится вероятность р того, что величина, имеющая распределение c2 с r степенями свободы, превзойдет данное значение c2. Вероятность р есть вероятность того что за счет чисто случайных причин мера расхождения теоретического и эмпирического распределений должна быть не меньше, чем полученная по результатам измерения.
Если серия измерений выполнена качественно, систематические погрешности исключены, то вероятность р, превышающая 0,2, может рассматриваться как не столь малая, при которой рассматриваемую гипотезу можно считать правдоподобной. И наоборот, если вероятность р велика, например, 0,95, то следует с настороженностью подойти к принятию гипотезы, если число измерений не равно 300 … 500.
Прямыми называются измерения, результат которых позволяет непосредственно получить искомое значение величины.
Равноточными (равнорассеянными) называются прямые независимые измерения постоянной величины, результаты которых могут рассматриваться как случайные, распределенные по одному и тому же закону.
В большинстве случаев при обработке прямых равноточных измерений исходят из предположения нормального закона результатов и погрешностей измерений.
По результатам серии снятия отсчетов по формуле (1) вычисляется наилучшая оценка математического ожидания 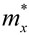 (среднее арифметическое).
(среднее арифметическое).
Если известна систематическая погрешность и она постоянна, то ее исключают из найденной величины математического ожидания.
По формуле (3) определяется наилучшая оценка СКО Sx (статистическая).
Помимо значений 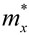 и Sx как точечных оценок при обработке результатов прямых равноточных измерений пользуются также интервальными оценками. Задав значение доверительной вероятности tx (из ряда 0,90, 0,95, 0,99), результат измерений записывают в виде
и Sx как точечных оценок при обработке результатов прямых равноточных измерений пользуются также интервальными оценками. Задав значение доверительной вероятности tx (из ряда 0,90, 0,95, 0,99), результат измерений записывают в виде
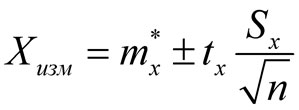 , , |
(10) |
Косвенное измерение – измерение, при котором значение физической величины определяют на основании результатов прямых измерений других физических величин, функционально связанных с искомой.
Пусть требуется оценить значение величины Y, связанной с измеренными величинами X1… Xi … Xk некоторой функциональной зависимостью
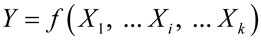 ,
,
где Х1, Хi, Хk – переменные, являющиеся источником погрешностей при измерениях.
Если функция нелинейна используют метод линеаризации. По которому СКО результата измерений вычисляют по формуле
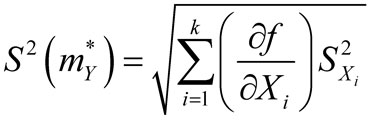 , , |
(11) |
Скачать программу
При небольшом количестве выполненных измерений (n < 10) обработка результатов не вызывает особых сложностей, она выполняется по формулам (1), (3), (10) для прямых измерений и (1), (11), (10) для косвенных измерений. При необходимости нахождения законов распределения, как уже отмечалось, необходимо выполнить большое количество измерений от 50 до 300 и более. Такое количество измерений обработать без использования компьютера оказывается весьма сложно.
Диалоговое окно программы представлено на рисунке 2.
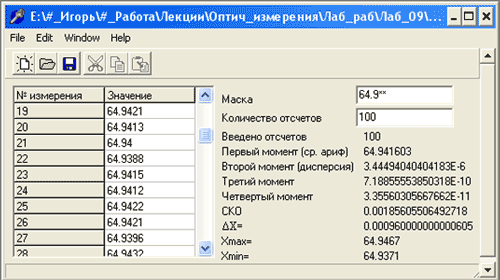
Рисунок 2 – Диалоговое окно программы статистической обработки результатов измерений
Перед началом ввода в таблицу экспериментальных данных следует задать количество отчетов. Для исключения необходимости ввода неизменяемой части следует использовать маску, которая состоит из неизменяемой и переменной части. Неизменяемая часть вводится в числовом виде, переменная в виде звездочек, например: 64.9**.
Результаты расчета и гистограмма (рисунок 3) обновляются в момент ввода значения.
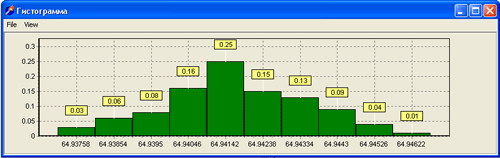
Рисунок 3 – Гистограмма погрешности выполненного измерения
Отчет по обработке результатов (рисунок 4) измерений выводится через меню Window выбором соответствующего пункта. Печать отчета по работе производиться через меню File/ Print Report.
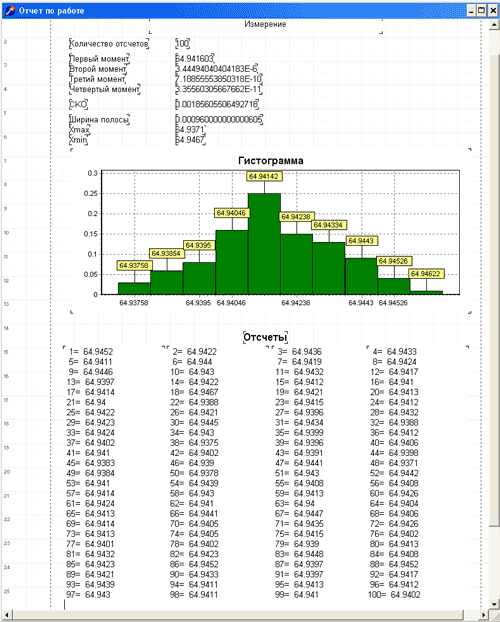
Рисунок 4 - Отчет по результатам измерений
Программа позволяет обработать большие массивы данных и получить численные значения не только 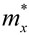 – первого момента,
– первого момента, 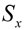 – статистического СКО, но и необходимую информацию для нахождения закона распределения по формулам (7), (9): Ii – границы i-го разряда, mi – количества значений, оказавшихся в i-ом разряде,
– статистического СКО, но и необходимую информацию для нахождения закона распределения по формулам (7), (9): Ii – границы i-го разряда, mi – количества значений, оказавшихся в i-ом разряде, 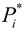 – статистические частоты (таблица 1).
– статистические частоты (таблица 1).
1. Кузнецов В.А., Ялунина Г.В. Основы метрологии. – М.: Издательство стандартов, –1995. – 279 с.
2. Селиванов М.Н., Фридман А.Э., Кудряшова Ж.Ф. Качество измерений. Метрологическая справочная книга. – Л.: Лениздат, –1987. – 295 с.