•ЛАБОРАТОРНЫЕ•

ПОРЯДОК ВЫПОЛНЕНИЯ РАСЧЕТОВ

Пример: вычислить координату и погрешность наведения. Идентифицировать закон распределения погрешностей по данным статистического ряда одному из теоретических законов распределения.

1.     В диалоговом окне (рисунок) установить необходимое количество отсчетов, в примере равное 100. В окно «маска» ввести неизменяемую часть чисел и изменяемую в виде ** (в примере 64.9***).

2.     В окно «значение» ввести данные эксперимента.

3.     При необходимости исключить промахи, которые на гистограмме выделяются красным цветом, а в таблице ввода словом "промах" (рисунок 1).

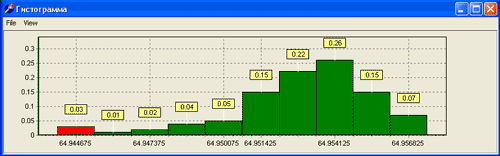
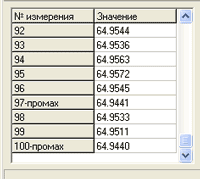
Рисунок 1 - Выделение промаха на гистограмме

4.     В примере вид гистограммы (рисунок) свидетельствует о том, что возможной теоретической моделью данного распределения является нормальный закон, который и принимается с целью идентификации.

5.     Данные расчета свести в статистический ряд (см. таблицу 1).

Ii	64,9371 64,9381	64,9381 64,9390	64,9390 64,9400	64,9400 64,9409	64,9409 64,9419	64,9419 64,9429	64,9429 64,9438	64,9438 64,9448	64,9448 64,9457	64,9457 64,9467
Di	64,9376	64,9385	64,9395	64,9405	64,9414	64,9424	64,9433	64,9443	64,9453	64,9462
mi	3	6	8	16	25	15	13	9	4	1
	0,03	0,06	0,08	0,16	0,25	0,15	0,13	0,09	0,04	0,01

6.     Найти среднее арифметическое значение погрешности по формуле

 

 

 

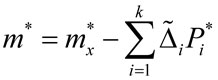
где 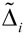  – среднее погрешности D в i-м разряде:

m^* = (64,941603-64,9376)×0,03+(64,941603-64,9385)×0,06+

+(64,941603-64,9395)×0,08+(64,941603-64,9405)×0,16+

+(64,941603-64,9414)×0,25+(64,941603-64,9424)×0,15+

+(64,941603-64,9433)×0,13+(64,941603-64,9443)×0,09+

+(64,941603-64,9453)×0,04+(64,941603-64,9462)×0,01=-0,000075 мм.

7.     Определить статистическую дисперсию по формуле

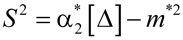,  где   .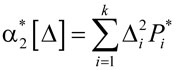

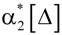  = (64,941603-64,9376)²×0,03+(64,941603-64,9385)²×0,06+

+(64,941603-64,9395)²×0,08+(64,941603-64,9405)²×0,16+

+(64,941603-64,9414)²×0,25+(64,941603-64,9424)²×0,15+

+(64,941603-64,9433)²×0,13+(64,941603-64,9443)²×0,09+

+(64,941603-64,9453)²×0,04+(64,941603-64,9462)²×0,01=0,000003499 мм².

Затем найти S² = 0,000003499-0,000075² = 0,000003493 мм². Статистическое СКО S = 0,001869201 мм.

8.     По формуле (7) и таблице функции Лапласа (приложение А) найти теоретические вероятности попадания случайной величины в каждом из разрядов:

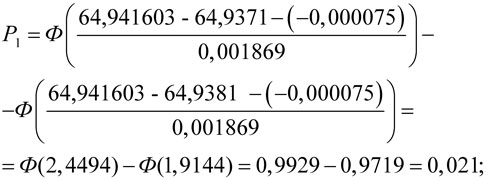
Р₂ = 0,048; Р₃ = 0,108; Р₄ = 0,153; Р₅ = 0,211; Р₆ = 0,194; Р₇ = 0,129; Р₈ = 0,082; Р₉ = 0,032; Р₁₀ = 0,012.

Сумма теоретических вероятностей должна быть равна 1. В примере 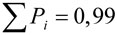, так как табличные аргументы функции Лапласа позволяют учесть только два разряда после запятой.

9.     С помощью формулы (9) определить меру расхождения:

10. Найти число степеней свободы распределения хи-квадрат с учетом того, достаточное число независимых условий для нормального закона распределения равно трем: r = k - s = 10 - 3 = 7.

11.  Из таблицы приложения Б в соответствии с числами c² = 3,475 и r = 7 определить значение вероятности сходимости эмперического и теоретического законов распределения р » 0,86.

12.  Вероятность р = 0,86 позволяет сделать вывод о том, что гипотеза о соответствии эмпирического закона нормальному закону распределения не противоречит экспериментальным данным.

13.  Результат экспериментальных данных при доверительной вероятности t_x = 0,9 записывается по формуле (10) и соответствует 64,9416±0,0002 мм.