Согласно закону преломления, луч света, падающий на границу раздела двух однородных изотропных сред, на границе раздела меняет свое направление, при этом падающий луч, луч преломленный и нормаль к поверхности в точке падения лежат в одной плоскости, а между углами падения и преломления существует зависимость (рисунок 45а):
 , |
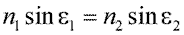где n1, n2 – показатели преломления оптических сред;
e1, e2 – углы падения и преломления луча.
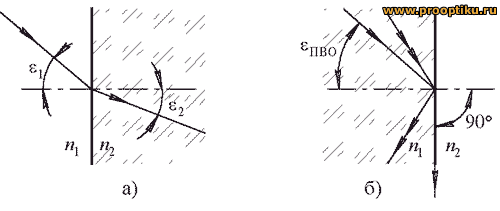
Рисунок 45 – К иллюстрации закона преломления
При распространении луча из оптически более плотной среды в менее плотную при некотором предельном угле падения eПВО угол преломления достигнет значения 90° (преломленный луч как бы распространяется вдоль границы раздела), при этом
 , |
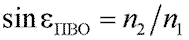Лучи, падающие на границу раздела двух сред (при n1 > n2) под углами меньше eПВО, преломятся и выйдут в среду с меньшим показателем преломления. Когда в более плотной среде угол падения превышает критическую величину eПВО, то преломления не наблюдается, а происходит полное внутреннее отражение (рисунок 45б).
Интенсивность потока энергии в волне, претерпевшей полное внутреннее отражение, в этом случае точно равна интенсивности потока в падающей волне, т. е. для углов, больших eкр, в среде с меньшим показателем преломления поток энергии равен нулю. Однако интенсивность поля в среде с меньшей плотностью отнюдь не равна нулю. Действительно, существует мгновенная, нормальная к границе раздела компонента потока энергии через границу, величина которой, усредненная по времени, равна нулю. Эта компонента не затухает в направлении распространения, но уменьшается экспоненциально с удалением от границы раздела [35].
М. Борн так описывает рассматриваемый процесс: «Хотя компонента вектора Пойнтинга в направлении, нормальном к границе, конечна, ее значение, усредненное по времени, равно нулю. Это означает, что не существует постоянного потока во вторую среду, а энергия течет туда и обратно» [36].
Рассмотрим часть энергии, отраженной от границы раздела, для волн, падающих под различными углами. Для этого воспользуемся известными формулами отражения Френеля. Для луча, падающего на границу раздела двух диэлектрических сред, и для двух плоскостей поляризации излучения эти формулы в общем виде записываются следующим образом:
 , |
 , |
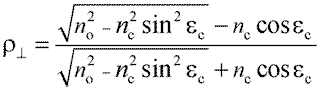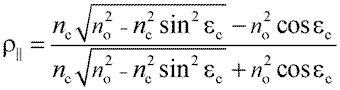где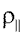 
и 
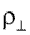– коэффициенты отражения для плоскостей поляризации, параллельной и перпендикулярной плоскости падения луча.
Здесь и далее индексы «с» и «о» в показателях преломления и углах падения относятся соответственно к средам с большим и меньшим показателем преломления (применительно к волокну – к сердцевине и оболочке).
Для неполяризованного света коэффициент отражения равен
 . |
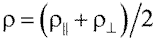На рисунке 46 [35] приведена зависимость коэффициента отражения Френеля от угла падения eс для nc = 1,5 и no = 1.
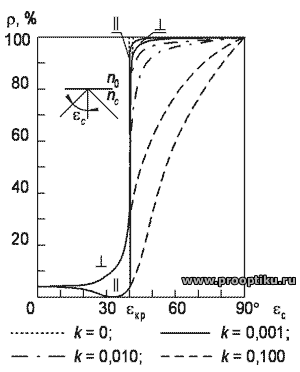
Рисунок 46 – Зависимость коэффициента отражения Френеля r от угла падения eс при различных k
Для углов, больших eкр, отражение теоретически равно 100% (коэффициент пространственного затухания волны k = 0). Ниже будет показано, что количество внутренних отражений в волокне может иногда превышать сотни тысяч. Из измерений действительного светопропускания волокон большой длины следует, что оно может быть близким к светопропусканию исходного материала той же длины. Отсюда вытекает, что коэффициент отражения близок 1 в пределах точности измерений. В работах Вейнберга и Саттарова показано, что в оптических волокнах может быть получен коэффициент единичного внутреннего отражения, равный 0,9999999.
Если одна из сред, на границе раздела которых происходит полное внутреннее отражение, имеет комплексный показатель преломления (nо - ik), то выражения коэффициента отражения для волн, поляризованных перпендикулярно и параллельно плоскости падения, принимают соответственно вид
и
 . |
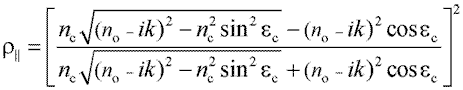При расчетах корень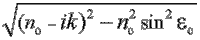 
берется в четвертом квадранте, и все величины возводятся в квадрат для получения абсолютных величин 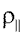и 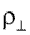. Влияние коэффициента пространственного затухания волны k на уменьшение коэффициента отражения приведено на рисунке 46, из которого видно, что при углах, больших критического, r заметно уменьшается даже для малых значений k.
