Рассмотрим механизм поглощения и распространения энергии вдоль волокна, представляющего собой прямой прозрачный цилиндр с плоским торцом (рисунок 47), окруженный оболочкой, при этом показатель преломления материала оболочки меньше показателя преломления материала сердцевины волокна: no < nc.
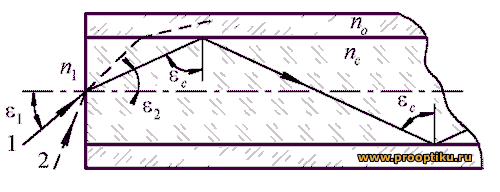
Рисунок 47–Прохождение луча вдоль прозрачного цилиндра с плоским торцом
Луч 1, падающий под углом e1, преломляется на входном торце под углом e2 к оси цилиндра и падает на стенку цилиндра под углом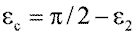 
. Если угол ec равен или больше 
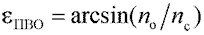, то этот луч претерпевает полное внутреннее отражение и падает на другую стенку цилиндра под тем же углом ec. Таким образом, луч удерживается внутри цилиндра, испытывая множество полных внутренних отражений, и выйдет из цилиндра только на противоположном торце. Для прямого круглого цилиндра угол падения меридионального луча на входе равен углу преломления на выходе. Однако если луч наклонен к оси волокна под углом, большим некоторого апертурного угла, например, луч 2 на рисунке 47, то после преломления на входном торце он падает на боковую поверхность под углом, меньшим eПВО, и уходит из цилиндра. Из формул Френеля следует, что некоторая часть энергии отражается даже в том случае, когда имеет место преломление. Однако очевидно, что после нескольких отражений и последующих преломлений эта часть энергии уменьшается до нуля внутри волокна. Таким образом, ясно, что существует предельный угол наклона лучей на входном торце цилиндра, величина которого обусловлена показателями преломления цилиндра и окружающей среды. Действительно, критический угол eПВО определяется из уравнения 
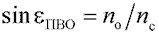. По закону преломления
 , |
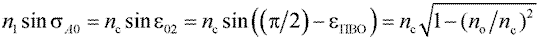где n1 – показатель преломления окружающей среды;
sА0 – угол падения лучей на входной торец волокна.
Следовательно, номинальная числовая апертура
 , |
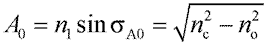(35) |
Поскольку номинальная числовая апертура относится к меридиональным лучам, то она довольно точно характеризует предельный угол наклона лучей на входе. Отметим, что после преломления на входном торце любой луч пройдет по стеклянному волокну при nc>1,5, находящемуся в воздухе, поскольку числовая апертура волокна в этом случае больше единицы (n1 = nо = 1). На рисунке 48 приведены кривые номинальной числовой апертуры в зависимости от отношения показателей преломления сердцевины и оболочки волокна для различных значений показателей преломления сердцевины волокна [35].
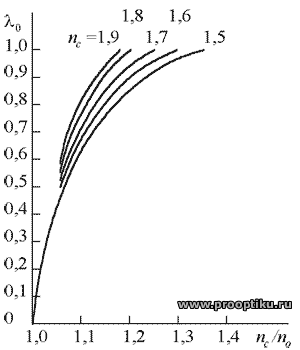
Рисунок 48 – Зависимость номинальной числовой апертуры волокна от отношения показателей преломления сердцевины и оболочки волокна
Как видно, чем больше nc, тем меньше отношение nc / no требуется для того, чтобы обеспечить тот же номинальный апертурный угол. Кривые рассчитаны для стеклянных волокон с оболочкой из стекла. Эта оболочка (с низким показателем преломления) в волоконно-оптических деталях служит для устранения потерь света, загрязнения на границе раздела «стекло – воздух» в волокнах без оболочки и для предотвращения утечки света из волокна в соседние волокна при тесном расположении их без оболочки. Кроме того, она играет роль связующей среды при изготовлении вакуумплотных изделий методом спекания волокон.
Очевидно, что если входная или выходная грани волокна не перпендикулярны оси волокна, а выполнены наклонно к оси, то это может вызвать уменьшение числовой апертуры, а при критических углах наклона выходного торца – и полное внутреннее отражение на нем.
Длину пути, пройденного меридиональным лучом вдоль прямого цилиндра, находящегося в воздухе, можно легко определить, представив схематически развертку волокна при каждом отражении. Из рисунка 49 наглядно видно, что длина пути P будет зависеть от длины волокна dc и угла e2 преломления луча на торце волокна: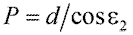 
.
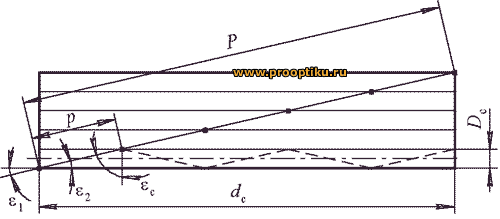
Рисунок 49 – К определению длины пути при прохождении волокна
Учитывая закон преломления на торце волокна и приняв n1 = 1, получим
 . |
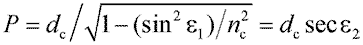(36) |
Выражение (36) свидетельствует о том, что длина пути зависит от угла падения луча, показателя преломления сердцевины волокна и длины волокна по оси, но не зависит от диаметра волокна.
Из рисунка 49 легко определяется и количество отражений h в волокне:
 , |
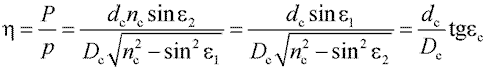(37) |
где Dc – диаметр волокна.
Заметим, что количество отражений зависит от диаметра волокна, причем, чем меньше диаметр волокна для данного наклона луча, тем больше количество отражений.
