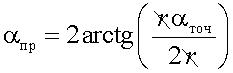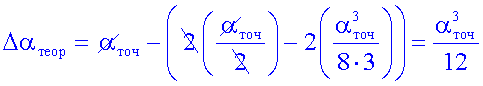• содержание • 1 • 2 • 3 • 4 • 5 • 5.1 • 5.2 • 6 • 6.1 • 6.2 • 6.3 • 6.4 • 6.5 • 6.6 • 7 • 7.1 • 7.2 • 7.3 • 7.4 • 7.5 • 7.6 • 8 • 8.1 • 8.2 • 8.3 • литература •

Если ФПД нелинейная, то следует проверить возможность использования приближенной линейной функции.

Теоретическая погрешность в общем виде определяется по формуле

,

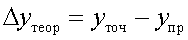(9)

где y_точ – точная ФПД;
       y_пр – приближенная ФПД.

Приближенную ФПД определим из формулы (8) по первому члену разложения ее в степенной ряд

,

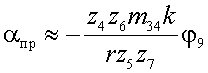(10)

Для упрощения записи введем обозначение

,

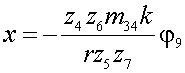Тогда из (8) точную функцию запишем как

,

Из (10) приближенную функцию запишем

,

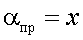На основании (9) запишем

,

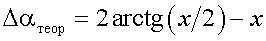(11)

Разложим функцию в степенной ряд на основании

где R_n(ξ) – остаточный член.

Можно воспользоваться справочником по высшей математике и взять формулу разложения функции в степенной ряд. Так для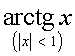

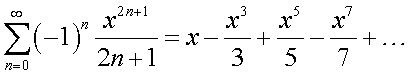
(12)

Ограничимся двумя первыми членами разложения и перепишем формулу (11)

.

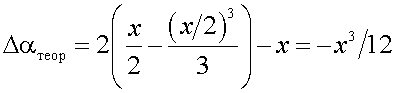Или после обратной замены получим формулу теоретической ошибки, учитывающей конструктивные параметры механизма

.

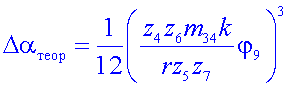(13)

Формулу теоретической ошибки можно получить другим путем.

Обращаем внимание на то, что нелинейная функция arctg появляется в формуле (2). Теоретическая погрешность механизма будет определяться этим выражением, будем считать, что она определяет приближенный закон движения

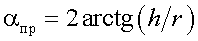
(14)

Точный закон запишем в виде

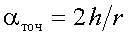
(15)

Из (15) выразим h

Полученное выражение подставим в (14)

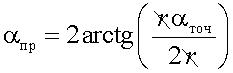
(16)

На основании (9) теоретическая погрешность определится из выражения

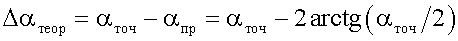
(17)

Разложим функцию 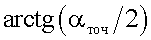в степенной ряд (см. (12)) и возьмем два первых члена разложения

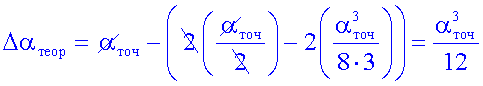
(18)

Полученное выражение (18) и выражение (13) идентичны, что будет подтверждено ниже.

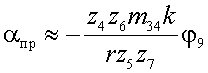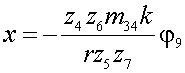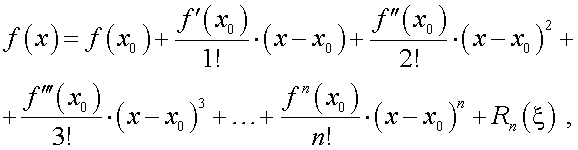
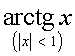
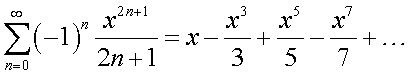
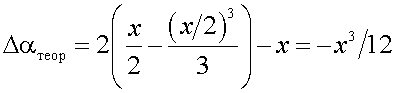• содержание • 1 • 2 • 3 • 4 • 5 • 5.1 • 5.2 • 6 • 6.1 • 6.2 • 6.3 • 6.4 • 6.5 • 6.6 • 7 • 7.1 • 7.2 • 7.3 • 7.4 • 7.5 • 7.6 • 8 • 8.1 • 8.2 • 8.3 • литература •