Используя данную элементную базу проанализируем возможность создания установок для измерения радиусов кривизны сферических полированных поверхностей. Один из вариантов установки представлен на рис. 21 [9].

Рисунок 21

В данном случае свет от источника света 1 проходит конденсор 2 и параллельным пучком равномерно освещает щель 3, установленную в передней фокальной плоскости объектива 4 коллиматора. Объектив коллиматора формирует широкий пучок параллельных лучей. Щели непрозрачного экрана 5, расположенные параллельно щели коллиматора и перпендикулярно плоскости чертежа, вырезают из широкого пучка два узких пучка лучей, симметричных оптической оси объектива. Расстояние между пучками равно 2r. Узкие пучки лучей падают на зоны контролируемой сферической поверхности и отражаются, исходя из правил геометрической оптики, под углом 2α, где α – угол падения пучка на контролируемую поверхность относительно нормали к поверхности в точке падения пучка лучей. Нормалью в данном случае является радиус кривизны поверхности. Если известно расстояние r и угол α, то по формуле

легко найти радиус кривизны поверхности. Так как нам известно расстояние r, то необходимо измерить только угол α.

Для этого контролируемый компонент располагается на столике 6, который может перемещаться вдоль оптической оси системы. Перемещение осуществляется при помощи электродвигателя 13. Измерение величины перемещения осуществляется при помощи датчика линейных перемещений 12. В отраженном ходе лучей устанавливается два позиционно-чувствительных фотоприемника 7 и 8, расстояние между разделительными гранями которых равно k.

Электродвигатель 13 осуществляет непрерывное перемещение столика вдоль оптической оси, а датчик линейных перемещений непрерывно выдает информацию о величине перемещения столика в блок обработки информации (арифметическое цифровое пересчетное устройство) 11. В результате этого в плоскости установки фотоприемников следы узких пучков лучей смещаются в горизонтальном направлении. При совмещении энергетического центра узкого пучка лучей с линией раздела фотоприемника 7 в блоке обработки информации фиксируется отсчет с датчика линейных перемещений. Затем след узкого пучка лучей смещается дальше и в момент, когда энергетический центр его совпадает с линией раздела фотоприемника 8, в блоке обработки информации фиксируется второй отсчет с датчика линейных перемещений. Разность этих отсчетов l равна величине перемещения столика, соответствующее перемещению следа узкого пучка лучей с одного фотоприемника на второй.

Из рисунка видно, что

,

откуда

.

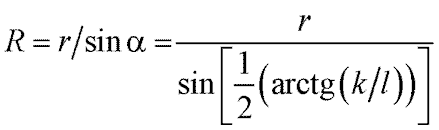(6)

Все вычисления производятся в блоке обработки информации по заданной программе, куда в качестве постоянных параметров вводятся значения r и k.

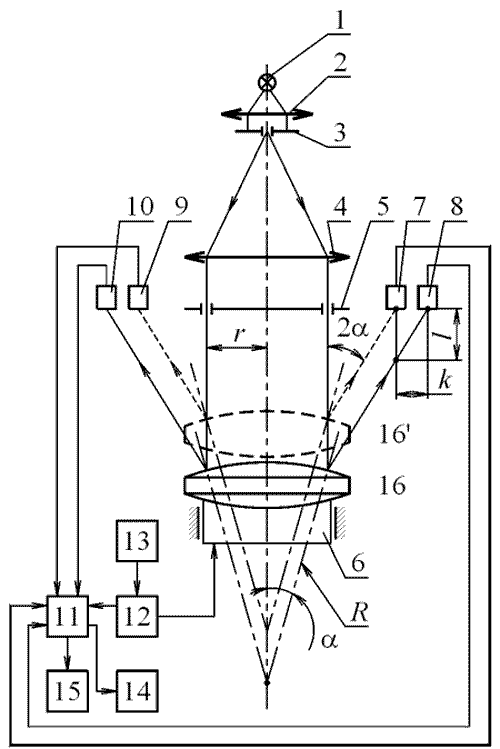
Как известно, отцентрировать контролируемую сферическую поверхность относительно оси коллиматора возможно с какой-то конечной точностью, т.е. контролируемая сферическая поверхность будет всегда децентрирована относительно оптической оси коллиматора. Вследствие этого будет вводиться погрешность в измерение угла α, а, следовательно, и в измеренное значение радиуса кривизны R.

Для устранения этой погрешности диаметрально противоположно приемникам 7 и 8 установлено два позиционно-чувствительных фотоприемника 9 и 10, расстояние между разделительными линиями которых также равно k. В результате этого в блоке обработки информации 11 фиксируется две пары отсчетов с датчика линейных перемещений и вычисляется два радиуса кривизны контролируемой поверхности, а затем его среднее значение.

Результаты измерений могут выводится на цифровое табло блока индикации 14 или ленту цифропечатающего устройства 15.

Время измерения фактически зависит только от времени перемещения столика из одного положения во второе и с учетом подготовительных операций составит величину порядка 10 сек.

Проведем анализ погрешности измерения на данной установке. Для этого примем R = 700 мм, r = 25 мм, k = 10 мм, l = 132,979 мм. В реальных условиях все параметры, входящие в расчетную формулу, будут измерены с какой-то погрешностью. Реально постоянные отрезки r и k можно измерить предварительно с малой погрешностью, порядка 0,002 мм. Поэтому примем Δr = 0,002 мм и Δk = 0,002 мм. Современные датчики линейных перемещений позволяют измерять линейные отрезки с погрешностью также порядка 0,002 мм, т. е. Δl = 0,002 мм.

На основании формулы (6) определим радиус кривизны контролируемой поверхности при номинальных значениях параметров

.

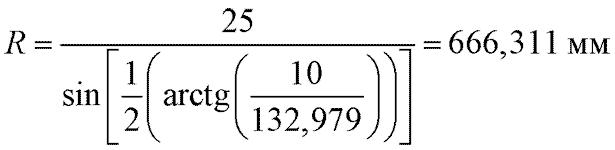Аналогичным образом определим радиус кривизны контролируемой поверхности при максимальном влиянии погрешностей параметров.

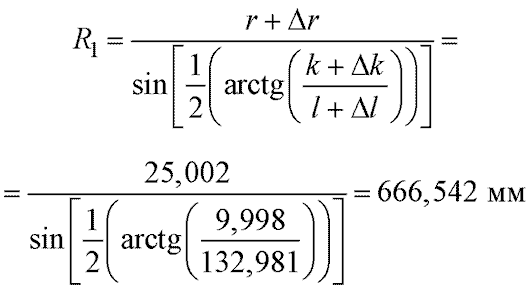
Откуда получим погрешность измерения

или

.

При измерении радиусов кривизны порядка 100 мм при тех же параметрах установки (r = 25 мм и k = 10 мм) величина перемещения будет равна 18, 064 мм.

Аналогично предыдущему по формуле (6) определим номинальное значение радиуса кривизны

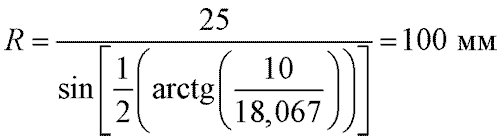
и радиус кривизны при максимальном влиянии погрешностей

,

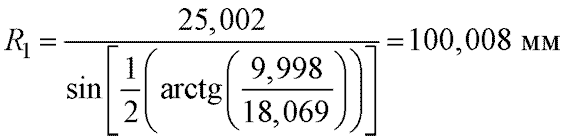откуда ΔR= 0,008 мм; ΔR/R = 0,008/100 = 0,00008 = 0,008%.

Как видно из проведенного анализа, предельная относительная погрешность определения радиуса кривизны зависит от величины радиуса. С ростом номинального значения радиуса кривизны погрешность возрастает, что характерно для подавляющего большинства методов измерения. Однако такая точность измерений является вполне удовлетворительной.

Следует отметить, что дополнительную погрешность в результаты измерения будет вносить непараллельность между собой двух узких пучков лучей, падающих на контролируемую поверхность. Для ее исключения необходим коллиматор с большим фокусным расстоянием и тщательная его юстировка, или учет ее влияния.

На данной установке принципиально можно измерять радиусы кривизны не только выпуклых, но и вогнутых сферических поверхностей. В этом случае узкие пучки параллельных лучей будут отклоняться к оптической оси системы и, поэтому, позиционно-чувствительные фотоприемники необходимо устанавливать в пределах перекрытой непрозрачным экраном центральной части объектива коллиматора (рис. 22). Установка будет работать в том же режиме.

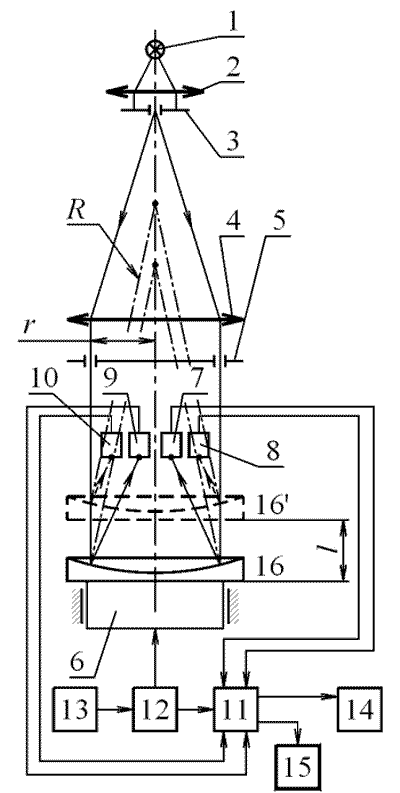
Рисунок 22

Следует, однако, отметить, что при измерении сравнительно небольших радиусов кривизны контролируемая поверхность должна располагаться ближе к объективу коллиматора.