Если в качестве непрозрачного экрана установить зеркало, повернутое зеркальным слоем в сторону контролируемой поверхности, то узкие пучки лучей будут трижды пересекать измерительную плоскость в точках a1, а2, а3, а4, а5, и a6 (рис. 30).
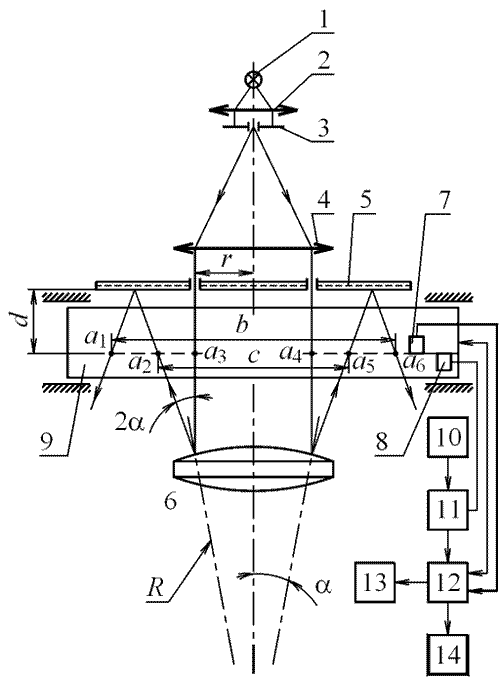
Рисунок 30
Если обозначить расстояние от зеркала до плоскости измерения через d/2 то, как и в предыдущем случае, можно измерять угол наклона узких пучков лучей относительно нормали к поверхности в точке падения пучков и производить контроль взаимной параллельности узких пучков лучей после непрозрачного экрана, а при необходимости, и вносить поправку в результаты измерения радиуса кривизны.
В этом случае два позиционно-чувствительных фотоприемника 7 и 8 устанавливаются на измерительной каретке таким образом, что их приемные площадки находятся в одной плоскости, перпендикулярной оптической оси системы и параллельной ходу каретки, но развернуты своими светоприемными площадками на 180°, т.е. фотоприемник 7 развернут в сторону контролируемой поверхности, а фотоприемник 8 – в сторону непрозрачного экрана 5.
Таким образом, при перемещении каретки 9 при помощи электродвигателя 10 в блоке обработки информации 12 будут зафиксированы отсчеты с датчика линейных перемещений при помощи фотоприемника 8 a1, а3, а4 и а6, а при помощи фотоприемника 7 – а2 и а5.
В данном случае обозначим a1 - а6 = b; а2 - а5 = с; а3 - а4 = е; 2r = k.
Тогда без учета влияния непараллельности узких пучков лучей формула для расчета радиуса кривизны контролируемой поверхности примет вид
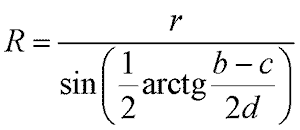
или с учетом влияния поправки на взаимную непараллельность узких пучков лучей следует использовать формулу (7).
Все расчеты производятся в блоке обработки информации 12 и результаты выводятся на цифровое табло блока индикации 14 или ленту цифропечатающего устройства 13.
Погрешность измерения будет того же порядка.
Данными методами можно успешно контролировать как выпуклые, так и вогнутые сферические поверхности.